A blog about technical writing, bioinformatics, and Python.
Posts
-
Independent Segregation of Chromosomes
This problem asks:
Given: A positive integer n ≤ 50.
Return: An array A of length 2n in which A[k] represents the common logarithm of the probability that two diploid siblings share at least k of their 2n chromosomes (we do not consider recombination for now).
-
Motzkin Numbers and RNA Secondary Structures
Wikipedia illustration of 21 ways to draw non-intersecting chords between 5 points on a circle.
This problem asks:
Given: An RNA string s of length at most 300 bp.
Return: The total number of noncrossing matchings of basepair edges in the bonding graph of s, modulo 1,000,000.
-
Comparing Spectra with the Spectral Convolution
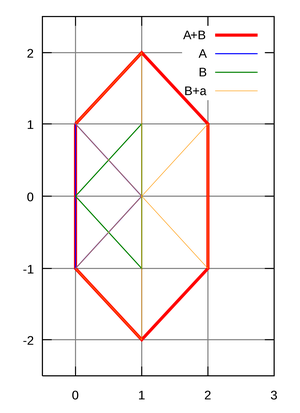
Minkowski sum image from Project Rosalind.
This problem asks:
Given: Two multisets of positive real numbers S1 and S2.
Return: The largest multiplicity of S1⊖S2, as well as the absolute value of the number x maximizing (S1⊖S2)(x)
-
Interleaving Two Motifs
This problem asks:
Given: Two DNA strings s and t.
Return: A shortest common supersequence of s and t.
-
Constructing a De Bruijn Graph
This problem asks:
Given: A collection of up to 1000 (possibly repeating) DNA strings of equal length (not exceeding 50 bp) corresponding to a set S of (k+1)-mers.
Return: The adjacency list corresponding to the de Bruijn graph corresponding to S∪Src.
-
Edit Distance Alignment
This problem asks:
Given: Two protein strings s and t.
Return: The edit distance dE(s,t) followed by two augmented strings s′ and t′ representing an optimal alignment of s and t.
-
Distances in Trees
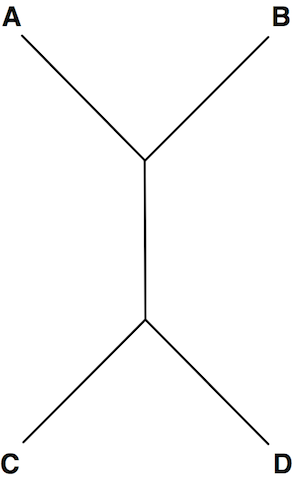
A simple tree that can be represented in Newick format as: (C, D, (A, B)); (A, (D, C), B); and (((A, B), C), D)
This problem asks:
Given: A collection of n trees (n≤40) in Newick format, with each tree containing at most 200 nodes; each tree Tk is followed by a pair of nodes xk and yk in Tk
Return: A collection of n positive integers, for which the kth integer represents the distance between xk and yk in Tk.
-
Introduction to Pattern Matching
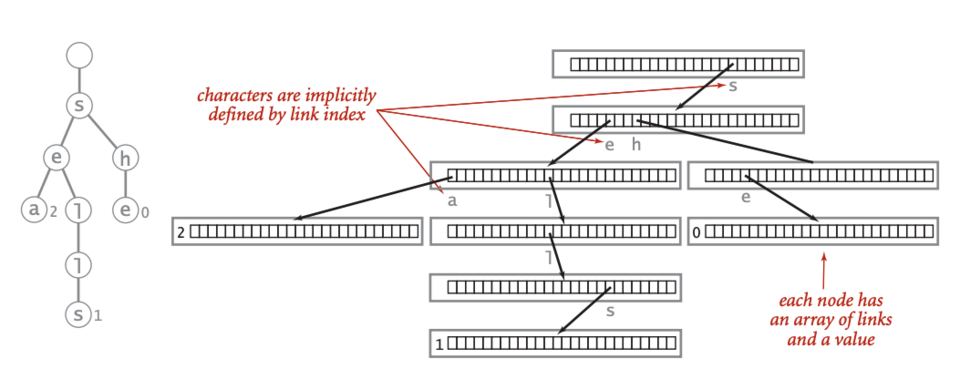
Trie representation from Wikipedia
This problem asks:
Given: A list of at most 100 DNA strings of length at most 100 bp, none of which is a prefix of another.
Return: The adjacency list corresponding to the trie T for these patterns, in the following format. If T has n nodes, first label the root with 1 and then label the remaining nodes with the integers 2 through n in any order you like. Each edge of the adjacency list of T will be encoded by a triple containing the integer representing the edge’s parent node, followed by the integer representing the edge’s child node, and finally the symbol labeling the edge.
-
Expected Number of Restriction Sites
This problem asks:
Given: A positive integer n (n≤1,000,000), a DNA string s of even length at most 10, and an array A of length at most 20, containing numbers between 0 and 1.
Return: An array B having the same length as A in which B[i] represents the expected number of times that s will appear as a substring of a random DNA string t of length n, where t is formed with GC-content A[i]
-
Inferring Protein from Spectrum
This problem asks:
Given: A list L of n (n≤100) positive real numbers.
Return: A protein string of length n−1 whose prefix spectrum is equal to L.
-
Introduction to Alternative Splicing
This problem asks:
Given: Positive integers n and m with 0≤m≤n≤2000.
Return: The sum of combinations C(n,k) for all k satisfying m≤k≤n, modulo 1,000,000.
-
Edit Distance
This problem asks:
Given: Two protein strings s and t
Return: The edit distance dE(s,t)
-
Maximum Matchings and RNA Secondary Structures
Screenshot of Project Rosalind not working.
This problem asks:
Given: An RNA string s of length at most 100.
Return: The total possible number of maximum matchings of basepair edges in the bonding graph of s.
-
Catalan Numbers and RNA Secondary Structures
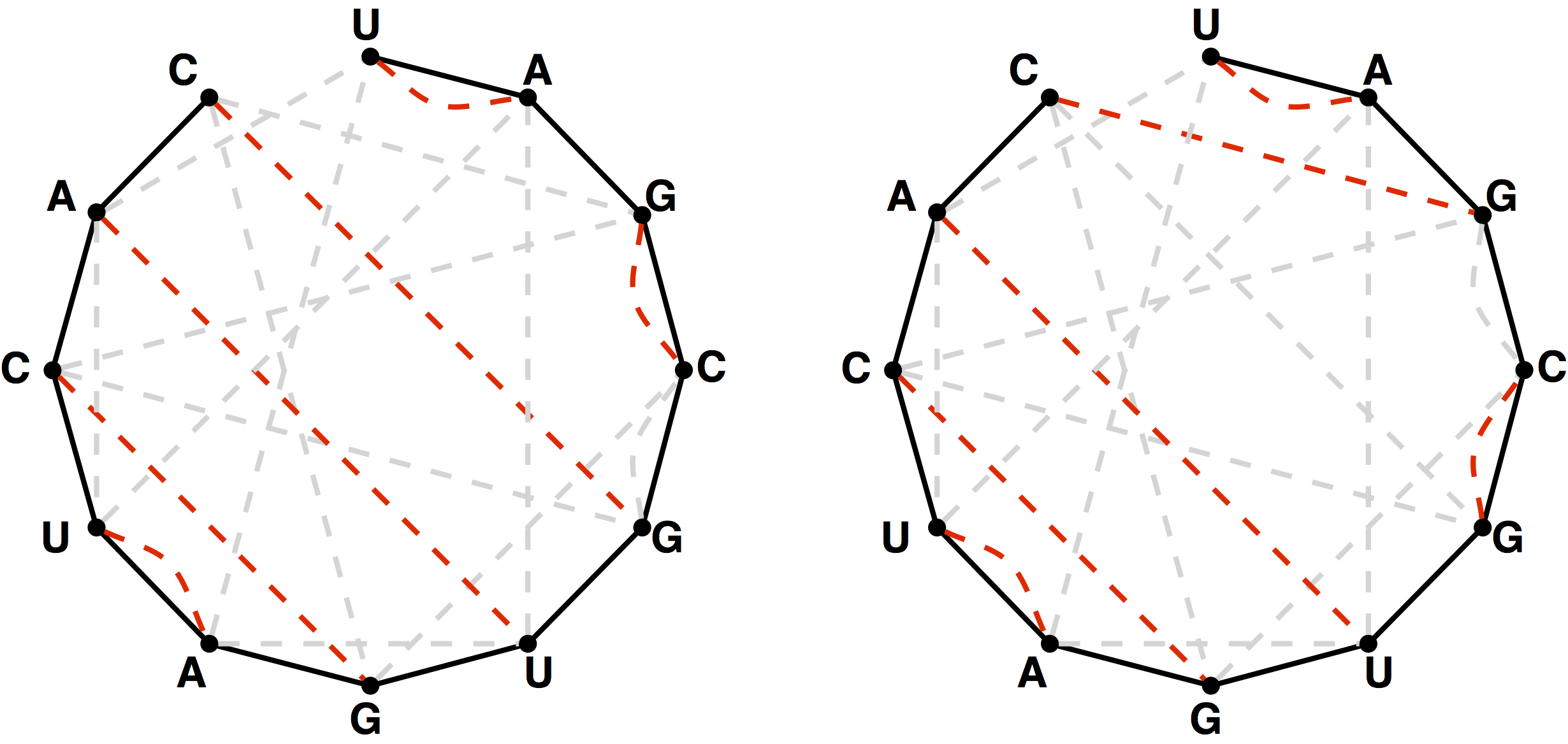
Figure 3 from this challenge on Project Rosalind
This problem asks:
Given: An RNA string s having the same number of occurrences of ‘A’ as ‘U’ and the same number of occurrences of ‘C’ as ‘G’.
Return: The total number of noncrossing perfect matchings of basepair edges in the bonding graph of s, modulo 1,000,000.
-
Introduction to Set Operations
This problem asks:
Given: A positive integer n (n≤20,000) and two subsets A and B of {1,2,…,n}.
Return: Six sets: A∪B, A∩B, A−B, B−A, Ac, and Bc (where set complements are taken with respect to {1,2,…,n}).
-
Error Correction in Reads
This problem asks:
Given: A collection of up to 1000 reads of equal length.
Return: A list of all corrections in the form “[old read]->[new read]”.
-
Finding a Shared Spliced Motif
Dynamic programming badge from Project Rosalind.
This problem asks:
Given: Two DNA strings s and t
Return: A longest common subsequence of s and t.
-
Creating a Distance Matrix
This problem asks:
Given: A collection of n (n≤10) DNA strings s1,…,sn of equal length (at most 1 kbp).
Return: The matrix D corresponding to the p-distance dp on the given strings.
-
Partial Permutations
This problem asks:
Given: Positive integers n and k such that 100≥n>0 and 10≥k>0.
Return: The total number of partial permutations P(n,k), modulo 1,000,000.
-
Speeding Up Motif Finding
This problem asks:
Given: A DNA string s.
Return: The failure array of s.
-
Counting Subsets
This problem asks:
Given: A positive integer n (n≤1000).
Return: The total number of subsets of {1,2,…,n} modulo 1,000,000.
-
k-Mer Composition
A 2-mer composition from Project Rosalind
This problem asks:
Given: A DNA string s.
Return: The 4-mer composition of s.
-
Genome Assembly as Shortest Superstring
This problem asks:
Given: At most 50 DNA strings of approximately equal length.
Return: A shortest superstring containing all the given strings.
-
Perfect Matchings and RNA Secondary Structures
This problem asks:
Given: An RNA string s of length at most 80 bp having the same number of occurrences of ‘A’ as ‘U’ and the same number of occurrences of ‘C’ as ‘G’.
Return: The total possible number of perfect matchings of basepair edges in the bonding graph of s.
-
Counting Phylogenetic Ancestors
This problem asks:
Given: A positive integer n (3≤n≤10000).
Return: The number of internal nodes of any unrooted binary tree having n leaves.
-
Enumerating Oriented Gene Orderings
This problem asks:
Given: A positive integer n≤6
Return: The total number of signed permutations of length n, followed by a list of all such permutations.
-
Completing a Tree
This problem asks:
Given: A positive integer n (n≤1000) and an adjacency list corresponding to a graph on n nodes that contains no cycles.
Return: The minimum number of edges that can be added to the graph to produce a tree.
-
Reversal Distance
This problem asks:
Given: A collection of at most 5 pairs of permutations, all of which have length 10.
Return: The reversal distance between each permutation pair.
-
Ordering Strings of Varying Length Lexicographically
This problem asks:
Given: A permutation of at most 12 symbols defining an ordered alphabet A and a positive integer n (n≤4).
Return: All strings of length at most n formed from A, ordered lexicographically.
-
Matching Random Motifs
This problem asks:
Given: A positive integer N≤100000, a number x between 0 and 1, and a DNA string s of length at most 10 bp.
Return: The probability that if N random DNA strings having the same length as s are constructed with GC-content x, then at least one of the strings equals s.
-
Longest Increasing Subsequence
This problem asks:
Given: A positive integer n≤10000 followed by a permutation π of length n.
Return: A longest increasing subsequence of π, followed by a longest decreasing subsequence of π.
-
Enumerating k-mers Lexicographically
This problem asks:
Given: A collection of at most 10 symbols defining an ordered alphabet, and a positive integer n (n≤10).
Return: All strings of length n that can be formed from the alphabet, ordered lexicographically
-
Transitions and Transversions
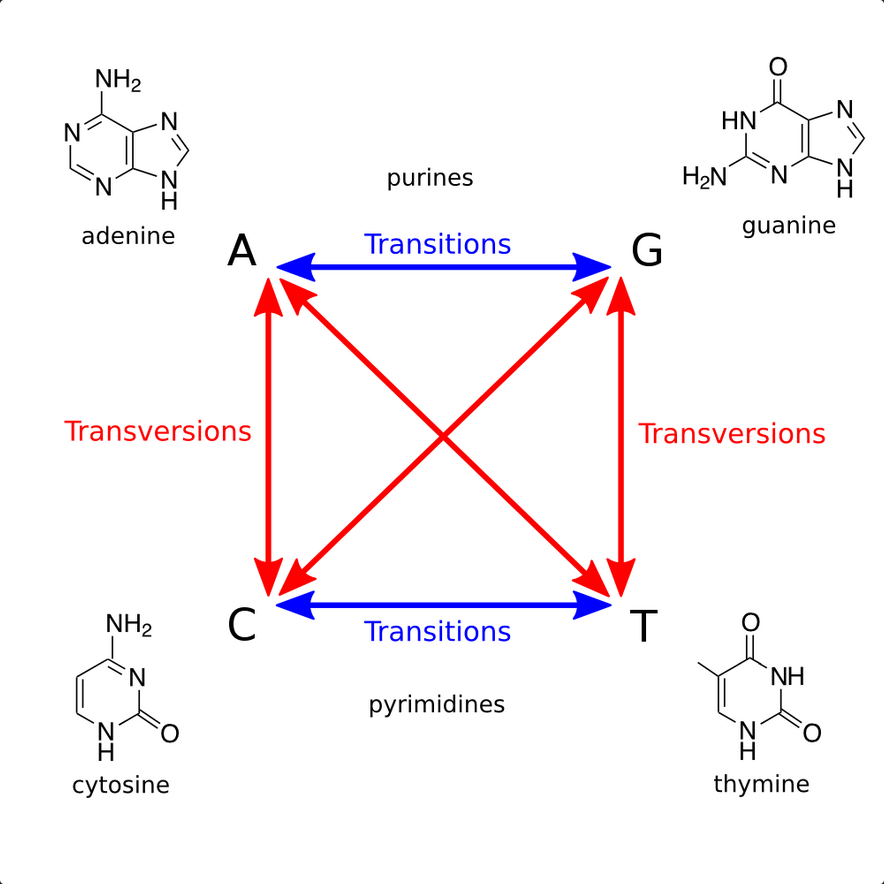
This problem asks:
Given: Two DNA strings s1 and s2 of equal length (at most 1 kbp).
Return: The transition/transversion ratio R(s1,s2).
-
Finding a Spliced Motif
This problem asks:
Given: Two DNA strings s and t.
Return: One collection of indices of s in which the symbols of t appear as a subsequence of s.
-
Introduction to Random Strings
This problem asks:
Given: A DNA string s of length at most 100 bp and an array A containing at most 20 numbers between 0 and 1.
Return: An array B having the same length as A in which B[k] represents the common logarithm of the probability that a random string constructed with the GC-content found in A[k] will match s exactly.
-
Locating Restriction Sites
This problem asks:
Given: A DNA string of length at most 1 kbp in FASTA format.
Return: The position and length of every reverse palindrome in the string having length between 4 and 12.
-
Enumerating Gene Orders
This problem asks:
Given: A positive integer n≤7
Return: The total number of permutations of length n, followed by a list of all such permutations (in any order).
-
Finding a Shared Motif
This problem asks:
Given: A collection of k (k≤100) DNA strings of length at most 1 kbp each in FASTA format.
Return: A longest common substring of the collection.
-
RNA Splicing
This problem asks:
Given: A DNA string s (of length at most 1 kbp) and a collection of substrings of s acting as introns.
Return: A protein string resulting from transcribing and translating the exons of s.
-
Open Reading Frames
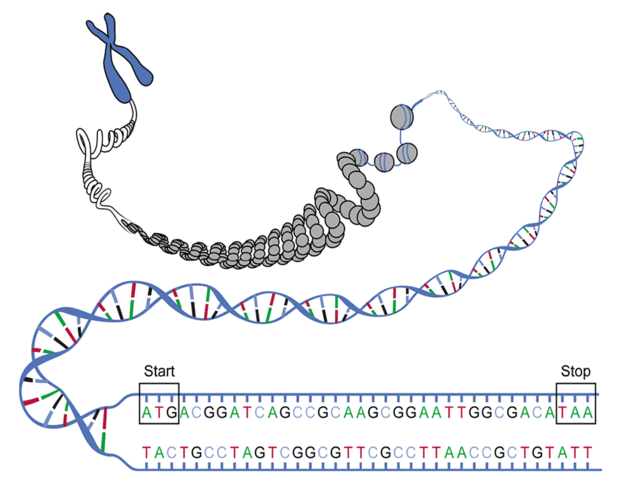
image from Project Rosalind.
This problem asks:
Given: A DNA string s of length at most 1 kbp in FASTA format.
Return: Every distinct candidate protein string that can be translated from ORFs of s.
-
Finding a Protein Motif
Error message seen in the course of solving this challenge.This problem asks:
Given: At most 15 UniProt Protein Database access IDs.
Return: For each protein possessing the N-glycosylation motif, output its given access ID followed by a list of locations in the protein string where the motif can be found.
-
Overlap Graphs
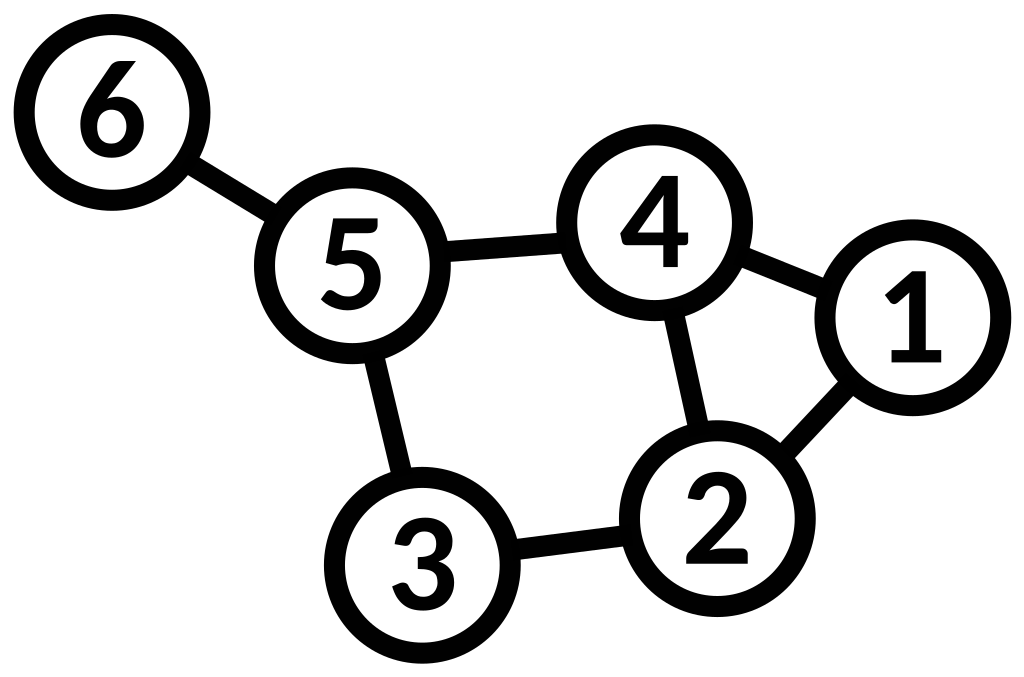
By Michel Bakni - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=151762031
This problem asks:
Given: A collection of DNA strings in FASTA format having total length at most 10 kbp.
Return: The adjacency list corresponding to O3. You may return edges in any order.
-
Consensus and Profile
Stephen Cole Kleene, inventor of regular expressions
This problem asks:
Given: A collection of at most 10 DNA strings of equal length (at most 1 kbp) in FASTA format.
Return: A consensus string and profile matrix for the collection.
-
Calculating Protein Mass
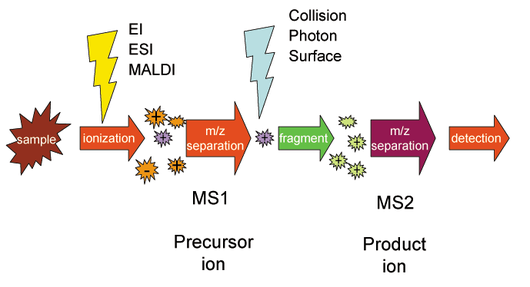
image of tandem mass spectrometry from Wikipedia
This problem asks:
Given: A protein string P of length at most 1000 aa.
Return: The total weight of P.
-
Independent Alleles
This problem asks:Given: Two positive integers k (k≤7) and N (N≤2k). In this problem, we begin with Tom, who in the 0th generation has genotype Aa Bb. Tom has two children in the 1st generation, each of whom has two children, and so on. Each organism always mates with an organism having genotype Aa Bb.
Return: The probability that at least N Aa Bb organisms will belong to the k-th generation of Tom’s family tree (don’t count the Aa Bb mates at each level). Assume that Mendel’s second law holds for the factors.
-
Translating RNA into Protein
This problem asks:
Given: An RNA string s corresponding to a strand of mRNA (of length at most 10 kbp).
Return: The protein string encoded by s.
-
Inferring mRNA from Protein
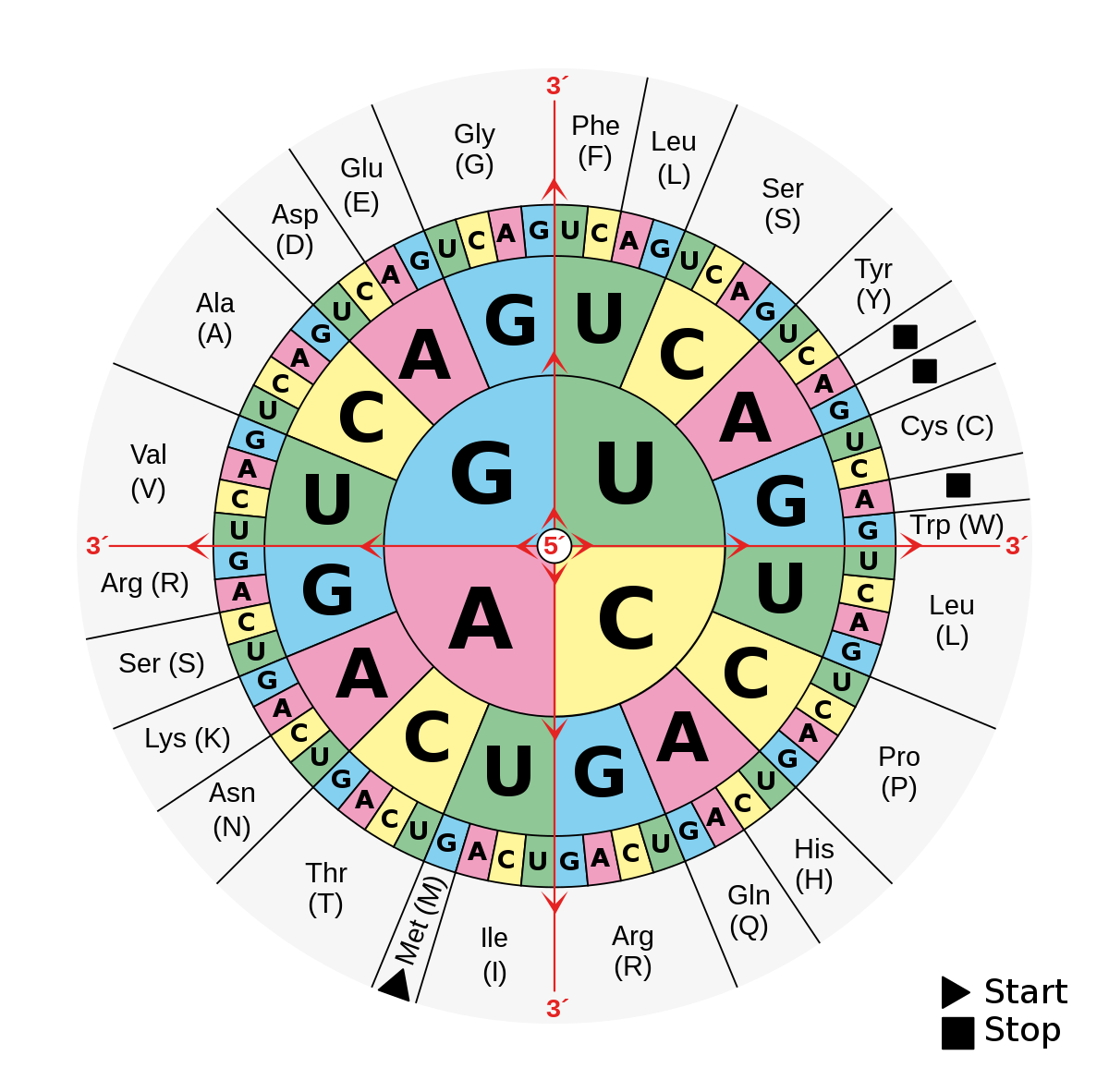
The standard RNA codon table organized in a wheel, from Wikipedia.
This problem asks:
Given: A protein string of length at most 1000 aa.
Return: The total number of different RNA strings from which the protein could have been translated, modulo 1,000,000.
-
Calculating Expected Offspring
This problem asks:
Given: Six non-negative integers, each of which does not exceed 20,000.
Return: The expected number of offspring displaying the dominant phenotype in the next generation, under the assumption that every couple has exactly two offspring.
-
Mortal Fibonacci Rabbits
This problem asks:
Given: Positive integers n≤100 and m≤20.
Return: The total number of pairs of rabbits that will remain after the n-th month if all rabbits live for m months.
-
Mendel's First Law
This problem asks:
Given: Three positive integers k, m, and n, representing a population containing k+m+n organisms: k individuals are homozygous dominant for a factor, m are heterozygous, and n are homozygous recessive.
Return: The probability that two randomly selected mating organisms will produce an individual possessing a dominant allele (and thus displaying the dominant phenotype). Assume that any two organisms can mate.
-
Finding a Motif in DNA
This problem asks:
Given: Two DNA strings s and t (each of length at most 1 kbp).
Return: All locations of t as a substring of s.
-
Counting Point Mutations
This problem asks:
Given: Two DNA strings s and t of equal length (not exceeding 1 kbp).
Return: The Hamming distance dH(s,t).
-
Rabbits and Recurrence Relations
This problem asks:
Given: Positive integers n≤40 and k≤5.
Return: The total number of rabbit pairs that will be present after n months, if we begin with 1 pair and in each generation, every pair of reproduction-age rabbits produces a litter of k rabbit pairs (instead of only 1 pair)
-
Computing GC Content
This problem asks:
Given: At most 10 DNA strings in FASTA format (of length at most 1 kbp each).
Return: The ID of the string having the highest GC-content, followed by the GC-content of that string.
-
Complementing a Strand of DNA
This problem asks:
Given: A DNA string s of length at most 1000 bp.
Return: The reverse complement s’c of s.
-
Transcribing DNA into RNA
This problem asks:
Given: A DNA string t having length at most 1000 nt.
Return: The transcribed RNA string of t
-
Counting DNA Nucleotides
This problem asks:
Given: A DNA string s of length at most 1000 nt.
Return: Four integers (separated by spaces) counting the respective number of times that the symbols ‘A’, ‘C’, ‘G’, and ‘T’ occur in s.
-
Welcome and Introduction
subscribe via RSS